An FRA is essentially an agreement to enter into two loans (one long, one short) in the future: a fixed-rate loan and a floating-rate loan. (The difference between an FRA and an actual agreement to enter into these two loans is that the FRA will be settled at the beginning of the loan period, whereas the loans would be settled at the end). Specifically, an m × n FRA is an agreement to enter into two (n – m)-month loans starting m months from today; i.e., the loan period starts m months from today and ends n months from today. For there to be no arbitrage opportunity, the price of an FRA, which is the agreed fixed rate, has to be the (n – m)-month forward rate starting m months from today; it’s the forward rate implied by the current spot rates for the expiration of the m × n FRA and the expiration of the underlying loans:
\[r_{fixed}\ =\ \left[ \frac{1\ +\ \left(S_n\dfrac{n\ ×\ 30}{360}\right)}{1\ +\ \left(S_m\dfrac{m\ ×\ 30}{360}\right)}\ -\ 1\right]\left[\frac{360}{\left(n\ –\ m\right)30}\right]\]
where:
- \(r_{fixed}\): fixed rate on FRA
- \(S_m\): m-month (LIBOR) spot rate
- \(S_n\): n-month (LIBOR) spot rate
Note that the formula above assumes that the rates are nominal rates, such as LIBOR.
For example, suppose that the 4-month (120-day) spot rate is 3%, and the 7-month (210-day) spot rate is 5%. Then the fixed rate on a 4 × 7 FRA – the 3-month (90-day) forward rate starting 4 months from now – would be:
\begin{align}_3f_4\ &=\ \left[\frac{1\ +\ \left(5\%\dfrac{7\ ×\ 30}{360}\right)}{1\ +\ \left(3\%\dfrac{4\ ×\ 30}{360}\right)}\ –\ 1\right]\left(\frac{360}{3\ ×\ 30}\right)\\
\\
&=\ 7.5908\%
\end{align}
(Look here if you need a refresher on calculating forward rates from spot rates.) This can perhaps best be visualized on a timeline:
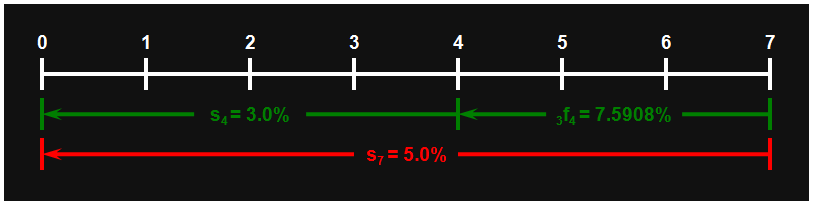
(Note: the remainder of this article explains the arbitrage transactions that ensure that the price has to be calculated according to the formula above. You can skip it if you care only what the formula is, not why it has to work.)
This (fixed) forward rate can be duplicated with fixed-rate bonds: being long the forward rate is equivalent to being long an n-month bond and short an m-month bond. Thus, the equivalent of being long a 7.5908%, 3-month loan starting 4 months from now (i.e., lending the money, and receiving the interest) is being short a 4-month, 3% bond (i.e., borrowing the money (issuing the bond) and paying the interest) and long a 7-month, 5% bond (i.e., lending the money (buying the bond) and receiving the interest). The par value on these bonds will be the present value of the loan starting in 4 months; the discount rate will be 3% (the 4-month spot rate). So, to duplicate a 3-month, $10,000,000 par, 7.5908% loan starting 4 months from now, you would sell a 4-month, 3% bond and buy a 7-month, 5% bond, each having a present value of:
\[\frac{$10,000,000}{1\ +\ \left(3\%\dfrac{4\ ×\ 30}{360}\right)}\ =\ $9,900,990\]
In 4 months, the payoff on the 4-month bond would be $10,000,000; to cover that, you will borrow $10,000,000 for 3 months at 7.5908%. At the end of that 3 months (7 months from today), you will have to repay the loan:
\[$10,000,000\left[1\ +\ \left(7.5908\%\frac{3\ ×\ 30}{360}\right)\right]\ =\ $10,189,769\]
However, at the end of 7 months you will be paid for the 7-month bond you bought today, and that payoff will be:
\[$9,900,990\left[1\ +\ \left(5\%\frac{7\ ×\ 30}{360}\right)\right]\ =\ $10,189,769\]
If the fixed rate on the FRA were anything other than the implied forward rate, an arbitrage opportunity would arise. The series of transactions is a little complicated – more so than for forwards, futures, and swaps – but not too bad.
Suppose that the FRA price were too high: 8%, say. Then we want to receive the 8% fixed rate on the FRA and pay the 7.5908% forward rate. Here are the arbitrage transactions (assume that in 4 months the 3-month LIBOR rate turns out to be 6%; the number doesn’t matter – the resulting arbitrage profit will be the same if it’s 6% or 7.5908% or 9.2% or anything else – but having a specific number will make the calculations easier to follow):
Today
- Sell a 7-month bond paying 5%, par value = $9,900,990
- Buy a 4-month bond paying 3%, par value = $9,900,990
- Enter into the short position (pay floating, receive fixed) on a $10,000,000 notional, 4 × 7 FRA, priced at 8%
Four months from today
- Receive the payoff on the 4-month bond: $10,000,000
- Buy a 3-month bond paying 6% (the current 3-month LIBOR rate), par value (and current price) = $10,000,000
- Receive the payoff on the FRA:
\[\frac{$10,000,000\left(8\%\ -\ 6\%\right)\dfrac{90}{360}}{1\ +\ 6\%\left(\dfrac{90}{360}\right)}\ =\ \frac{$50,000}{1\ +\ 6\%\left(\dfrac{90}{360}\right)}\ =\ $49,261\]
- Buy a 3-month bond paying 6%, par value (and current price) = $49,261
(Note: if the 3-month LIBOR rate were higher than 8%, the payoff on the FRA would be negative, and you would sell a 3-month bond instead of buying a 3-month bond.)
Seven months from today
- Receive the payoff on the 3-month, $10,000,000 bond: $10,150,000 (= $10,000,000 × (1 + 6%/4))
- Receive the payoff on the 3-month, $49,261 bond: $50,000 (the undiscounted FRA payoff)
- Pay off the 7-month bond: $10,189,769
- Arbitrage profit = $10,150,000 + $50,000 – $10,189,769 = $10,231
By buying the $10,000,000 bond at 6% you have neutralized the effect of the (previously unknown) market floating rate, and by buying the $49,261 bond at 6% you have effectively counteracted the discounting of the FRA payoff (which is why the actual LIBOR rate at the expiration of the FRA doesn’t matter), leaving only the (undiscounted) fixed rate. The effect of these transactions will be receiving the (high) FRA fixed rate and paying the forward rate (at the end of the loan period):
\[$10,000,000\left(8\%\ -\ 7.5908\%\right)\frac{90}{360}\ =\ $10,231\]
(If the 3-month LIBOR rate in 4 month were, say, 7%, the net result will be the same. The undiscounted payoff on the FRA would be $25,000, and the discounted payoff would be $24,570. You would buy a $10,000,000 par, 3-month bond paying 7% and a $24,570 par, 3-month bond paying 7% (each priced at par), and your payoff in 3 months would be $10,175,000 + $25,000 = $10,200,000, which is the same as what you would get when the 3-month LIBOR rate is 6%. As I stated, the 3-month LIBOR rate at the expiration of the FRA doesn’t matter; your profit is always the same amount.)
If the FRA price were too low, the arbitrage transactions would start (today) with:
- Sell a 4-month bond paying 3%, par value = $9,900,990
- Buy a 7-month bond paying 5%, par value = $9,900,990
- Enter into the long position (pay fixed) on a $10,000,000 notional, 4 × 7 FRA
(I leave the remainder of the transactions to your imagination.)
